
Have you ever wondered what exactly the single pixels of a QR code mean? How you could generate your own QR code by hand?
In this post, we will decode by hand the QR Code on the right, which links to https://jbirnick.github.io/ and was created with some online generator.
Overview
The pixels of a QR code can be grouped into the following 4 (or 5) categories:

- function patterns
- format information
- version information
- data codewords & error correction codewords, modulo mask
- (blank, modulo mask)
Of course, in the end, we are interested in the data codewords. The error correction codewords help to reconstruct the data codewords in case a few pixels are lost or erroneous. A mask is applied there to avoid e.g. big areas of white pixels (which are hard to scan) that might come from the data. The version information contains the size of the QR code. The format information contains the level of error correction and the ID of the used mask. And the function patterns are just there to help the camera find and scan the QR code.
Function Patterns

Each QR code has three corners with the same 7px times 7px finder pattern. Towards the inner side of the QR code, they have a white 1px wide separator. This helps the camera to locate the QR code (boundaries).
But QR codes can become quite large, as they come in 40 different sizes, called “versions”. Version 1 has a sidelength of 21px, version 40 has sidelength 177px, and inbetween it goes in steps of 4px. Our QR code has a sidelength of 25px, so it’s of version 2.
So there are additional patterns to help the camera read the pixels. Between the finder patterns are 1px wide alternating timing patterns. Furthermore, there are 5px times 5px alignment patterns distributed across the QR code. Their quantity and position depend on the version; in our case, there is only one.
Format Information

You can see that I marked 30 bits as format information. Actually, there are only 15 bits, which are printed twice as in the picture below, and the pixel above the lower 7th pixel is (always) black.
Of those 15 bits, in turn, only the first 5 are relevant; the latter 10 are just for error correction.
These first 5 bits shall be XORed with 10101, and can then be decoded as follows.
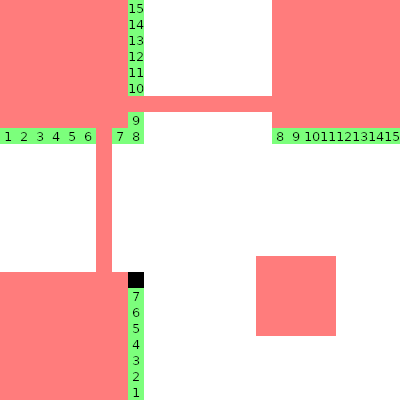
The first 2 bits indicate the error correction level (see later) according to this table:
| EC Level | Format Info |
|---|---|
| L | 01xxx |
| M | 00xxx |
| Q | 11xxx |
| H | 10xxx |
The last 3 bits indicate the mask which is applied to the data & error correction codewords.
Let’s analyze it in our case.
The raw first 5 bits are 11010, so after the obligatory XOR with 10101 we obtain 01111.
This means we have error correction level L and mask 111 (which you’ll see later).
Version Information
Our QR code doesn’t contain version information, because this is only included in version 7 and larger. It would just contain the version number (i.e. size) of the QR code (and, as the format information, some error correction bits). Similar to the format information, two copies are placed into the QR code: one above the bottom left finder pattern, and another to the left of the top right finder pattern.
Data & Error Correction Codewords

The rest of the space is (finally!) taken for codewords.
But first, recall that we need to apply mask 111.

You can see it on the left. Applied to our QR code, except for function patterns and format info and version info, it yields the second picture on the right.

Now in which order should we read the bits? We go:
- in columns of width 2 from right to left in an up-down-up-down-… pattern
- within a column, always first right then left
- function patterns are skipped
There is one little exception: The timing pattern between the two finding patterns on the left is “completely skipped”. Please see the first picture below to grasp what I mean.
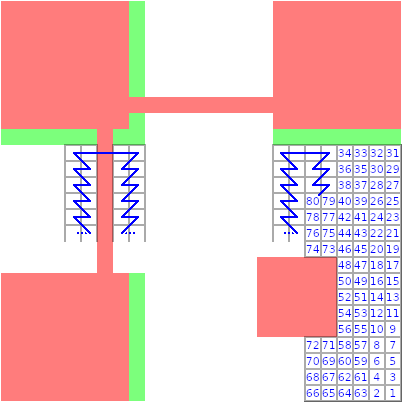
Now these bits are divided into codewords of 8 bits each. Since we have 359 bits (check!), we can put 44 codewords and need to leave 7 bits blank.
The allocation of the codewords and the numbering of the bits within them is shown below.


Our codewords are:
01: 0b01110001 = 0x7102: 0b10100100 = 0xA403: 0b00011011 = 0x1B04: 0b01101000 = 0x6805: 0b01110100 = 0x7406: 0b01110100 = 0x7407: 0b01110000 = 0x7008: 0b01110011 = 0x7309: 0b00111010 = 0x3A10: 0b00101111 = 0x2F11: 0b00101111 = 0x2F12: 0b01101010 = 0x6A13: 0b01100010 = 0x6214: 0b01101001 = 0x6915: 0b01110010 = 0x7216: 0b01101110 = 0x6E17: 0b01101001 = 0x6918: 0b01100011 = 0x6319: 0b01101011 = 0x6B20: 0b00101110 = 0x2E21: 0b01100111 = 0x6722: 0b01101001 = 0x6923: 0b01110100 = 0x7424: 0b01101000 = 0x6825: 0b01110101 = 0x7526: 0b01100010 = 0x6227: 0b00101110 = 0x2E28: 0b01101001 = 0x6929: 0b01101111 = 0x6F30: 0b00101111 = 0x2F31: 0b00000000 = 0x0032: 0b11101100 = 0xEC33: 0b00010001 = 0x1134: 0b11101100 = 0xEC35: 0b00010101 = 0x1536: 0b00100011 = 0x2337: 0b01010010 = 0x5238: 0b01110010 = 0x7239: 0b00100111 = 0x2740: 0b01100000 = 0x6041: 0b10110010 = 0xB242: 0b00011001 = 0x1943: 0b11100111 = 0xE744: 0b10100011 = 0xA3
You can see that I highlighted the codewords in two different colors. This is because we have error correction level L, which means that of our 44 codewords, (the first) 34 contain the data and 10 are for error correction.
Before we decode the data, let’s check how the error correction is constructed.
Error Correction
For error correction, each codeword is interpreted as an element of $$\F_2[t]/(t^8 + t^4 + t^3 + t^2 + 1) \cong: \F_{2^8} = \F_2(\alpha)$$ with $\alpha := \bar{t}$. Namely, the codeword $b_7 b_6 \cdots b_0$ is interpreted as $b_7 \alpha^7 + \dots + b_0$.
(For non-mathematicians: $\F_q$ is the finite field with $q$ elements.)
Now we form a polynomial $D \in \F_{2^8}[X]$ whose coefficients are the data codewords (interpreted as elements of $\F_{2^8}$). The first data codeword is the coefficient of $X^{33}$ and the 34th (i.e. last) data codeword is the constant coefficient.
Hence the whole data (and nothing more) is captured in the polynomial $D$.
Now we compute $D \cdot X^{10}$ modulo $g$ where $g \in \F_{2^8}[X]$ is the polynomial
$$ \begin{align*} g &= \prod_{i=0}^9 (X-\alpha^i) \\ &= X^{10} + \alpha^{251} X^9 + \alpha^{67} X^8 + \alpha^{46} X^7 + \alpha^{61} X^6 + \alpha^{118} X^5 \\ &\quad + \alpha^{70} X^4 + \alpha^{64} X^3 + \alpha^{94} X^2 + \alpha^{32} X + \alpha^{45} \end{align*} $$of degree 10. This yields a polynomial $E \in \F_{2^8}[X]$ of degree 9. Similar to how we constructed the data polynomial $D$, this is in turn used to construct the error correction codewords. The coefficient of $X^9$ in $E$ will form the first error correction codeword (so codeword 35), and the constant coefficient of $E$ will form the last error correction codeword (codeword 44).
This can be considered a BCH variant of Reed-Solomon error correction. I might explain in a later series how to actually correct errors with this (and what this means).
But let’s check that in our QR code this is what actually happened. We have
$D = (\alpha^{6} + \alpha^{5} + \alpha^{4} + 1) X^{33} + (\alpha^{7} + \alpha^{5} + \alpha^{2}) X^{32} + (\alpha^{4} + \alpha^{3} + \alpha + 1) X^{31} + (\alpha^{6} + \alpha^{5} + \alpha^{3}) X^{30} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha^{2}) X^{29} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha^{2}) X^{28} + (\alpha^{6} + \alpha^{5} + \alpha^{4}) X^{27} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha + 1) X^{26} + (\alpha^{5} + \alpha^{4} + \alpha^{3} + \alpha) X^{25} + (\alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha + 1) X^{24} + (\alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha + 1) X^{23} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha) X^{22} + (\alpha^{6} + \alpha^{5} + \alpha) X^{21} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + 1) X^{20} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha) X^{19} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha) X^{18} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + 1) X^{17} + (\alpha^{6} + \alpha^{5} + \alpha + 1) X^{16} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha + 1) X^{15} + (\alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha) X^{14} + (\alpha^{6} + \alpha^{5} + \alpha^{2} + \alpha + 1) X^{13} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + 1) X^{12} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha^{2}) X^{11} + (\alpha^{6} + \alpha^{5} + \alpha^{3}) X^{10} + (\alpha^{6} + \alpha^{5} + \alpha^{4} + \alpha^{2} + 1) X^{9} + (\alpha^{6} + \alpha^{5} + \alpha) X^{8} + (\alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha) X^{7} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + 1) X^{6} + (\alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha + 1) X^{5} + (\alpha^{5} + \alpha^{3} + \alpha^{2} + \alpha + 1) X^{4} + (\alpha^{7} + \alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha^{2}) X^{2} + (\alpha^{4} + 1) X + \alpha^{7} + \alpha^{6} + \alpha^{5} + \alpha^{3} + \alpha^{2}$
and so $D \cdot X^{10}$ modulo $g$ gives:
$E = (\alpha^4 + \alpha^2 + 1) X^9 + (\alpha^5 + \alpha + 1) X^8 + (\alpha^6 + \alpha^4 + \alpha) X^7 + (\alpha^6 + \alpha^5 + \alpha^4 + \alpha) X^6 + (\alpha^5 + \alpha^2 + \alpha + 1) X^5 + (\alpha^6 + \alpha^5) X^4 + (\alpha^7 + \alpha^5 + \alpha^4 + \alpha) X^3 + (\alpha^4 + \alpha^3 + 1) X^2 + (\alpha^7 + \alpha^6 + \alpha^5 + \alpha^2 + \alpha + 1) X + \alpha^7 + \alpha^5 + \alpha + 1$
You can check that this actually agrees with the error correction codewordes above.
Data Decoding
Finally, let’s decode the data codewords.
The first 4 bits indicate the mode (Numeric, Alphanumeric, Byte, Kanji, …).
We have 0111, which means ECI (Extended Channel Interpretation) mode.
The next 8 bits (i.e. the last 4 bits of codeword 1 and the first 4 bits of codeword 2) contain the ECI Designator 0x1A, which means that UTF-8 encoding is used.
The 4 bits after this (i.e. the last 4 bits of codeword 2) contain the mode in which the data is encoded.
In our case, 0100, this means we use byte mode.
(This is kinda the default, we just read the bytes and nothing more.
Other modes exist as shortcuts to often-used byte ranges.)
Codeword 3 contains the character count, namely 27.
Codewords 4 to 30 then encode the string https://jbirnick.github.io/ in UTF-8.
In this case, each character takes only one codeword.
Codeword 31 is 00000000, the terminator.
We still have three free codewords.
They are filled up by alternately adding the pad codewords 11101100 and 00010001.